 第1章双变量回归分析.ppt
第1章双变量回归分析.ppt
《第1章双变量回归分析.ppt》由会员分享,可在线阅读,更多相关《第1章双变量回归分析.ppt(50页珍藏版)》请在优知文库上搜索。
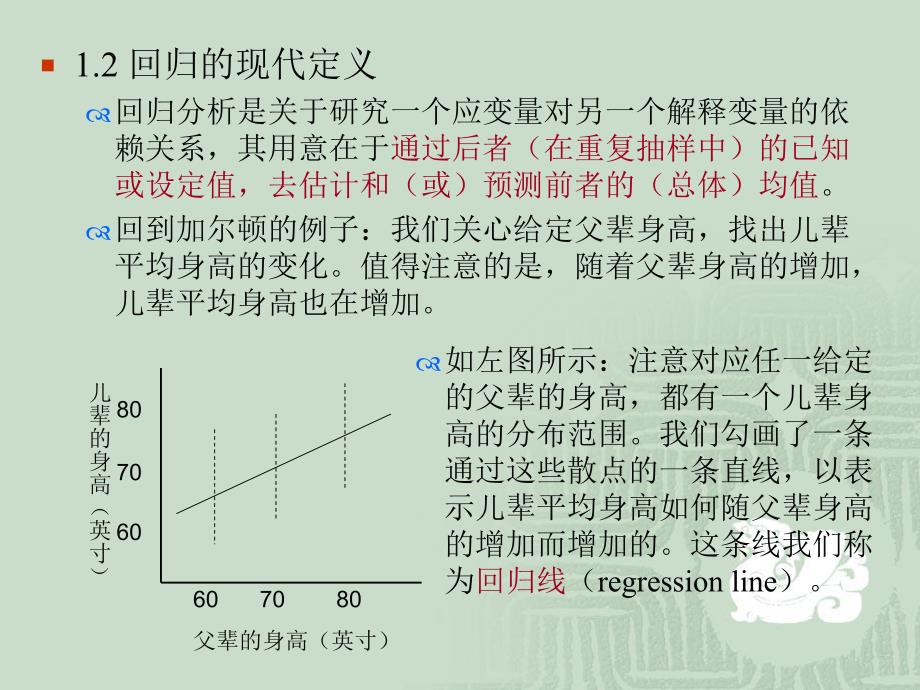
1、经济类核心课程计量经济学第一章 双变量回归分析1.回归分析的性质F.加尔顿(Francis Galton)发现,虽然有一个趋势:父母高,儿女也高;父母矮,儿女也矮,但给定父母的身高,儿女辈的平均身高却趋向于或者“回归”到全体人口的平均身高。K.皮尔逊(Karl Pearson)证实了加尔顿普遍回归定律。皮尔逊收集了1000多个家庭的身高记录。他发现对于父辈高的群体,儿辈的平均身高低于他们的父辈,而对于父辈矮的群体,儿辈的平均身高则高于他们的父辈。用加尔顿的话来说,就是“回归到中等(regression to mediocrity)”。1.2 回归的现代定义回归分析是关于研究一个应变量对另一个解
2、释变量的依赖关系,其用意在于通过后者(在重复抽样中)的已知或设定值,去估计和(或)预测前者的(总体)均值。回到加尔顿的例子:我们关心给定父辈身高,找出儿辈平均身高的变化。值得注意的是,随着父辈身高的增加,儿辈平均身高也在增加。60 70 80父辈的身高(英寸)儿辈的身高(英寸)807060如左图所示:注意对应任一给定的父辈的身高,都有一个儿辈身高的分布范围。我们勾画了一条通过这些散点的一条直线,以表示儿辈平均身高如何随父辈身高的增加而增加的。这条线我们称为回归线(regression line)。1.3 统计关系和确定性关系如上例中,我们不像经典物理学中考虑的那种变量之间的函数或确定性依赖关系
3、。在回归分析中,我们考虑的是一类所谓统计依赖关系。在变量之间的统计关系中,我们主要处理是随机变量,也就是有着概率分布的变量。例如,作物收成对气温、降水、阳光及施肥的依赖关系是统计性质的。这个性质的意义在于:这些解释变量固然重要,但是并不能够使农业学家准确地预测作物的收成。一则这些变量的测量是有误差的,二则还有一大堆影响到作物收成的变量,我们无法一一识别出来。1.4 回归和因果关系虽然回归分析是研究一个变量对另一些变量的依赖关系,但它并不一定意味着因果关系。用肯达尔和斯图亚特的话说:“一个统计关系式,无论多强也不管多么有启发性,却永远不能确立因果方面的联系,对因果关系的理念,必须来自统计学以外,
4、最终来自这种或那种理论。”例如在诸多有趣的经济指标中有一个“裙子长短指数”。这个指数用女性穿着裙子的长短来判断经济的好坏。当经济不好时,失业率增加,女性就业更困难,短裙看起来能年轻、活力一些,有利于寻求新的职位。但是我们不能因此得到结论:在座的女生穿着短裙是因为经济不好,或者因为在座的女生穿着短裙所以中国的经济不好。从逻辑上说,统计关系式本身不意味着任何因果关系。1.5 数据的性质用于经济分析的数据有三类:时间序列、横截面数据、和混合数据。时间序列:对一个变量在不同时期取值的一组观测结果。例如随着年份GDP的变换、上证综合指数的每日变换等等。基于时间序列数据的计量分析,大多假定所依据的时间序列
5、数据是平稳的(stationary)。粗略地来说,如果一组时间序列数据,它们的均值和方差在时间上没有系统的变化,就是平稳的。要记住:每当你使用时间序列数据时,你都要问一问它的平稳性如何。横截面数据:对一个或多个变量在同一个时点上收集的数据。例如2012年9月份,全国主要30个省份的生猪的产量和价格、全国每个高校2012届大学生的就业率等等。横截面数据也有其自身的问题,特别是异方差(heterogeneity)的问题。有的省(湖南、江西)生产巨量的生猪,而有的省(北京和广东)生产量很少。当我们的统计分析中包含有相异的单元时,我们必须考虑尺度效应,以避免把苹果和桔子混同了起来。混合数据:兼有时间序
6、列和横截面数据。例如人口普查数据,从1980到2012年中国人口总量变化是时间序列,而2012年不同省市人口的分布则是横截面数据。2.双变量回归分析2.1 一个例子假定一个国家人口总体由60户家庭组成,X表示家庭周可支配收入,Y表示家庭周消费支出。X,每周家庭收入(美元)Y,每周家庭消费支出8010012014016018020022024026055657980102110120135137150607084931071151361371451526574909511012014014015517570809410311613014415216517875859810811813514515
7、717518088113125140160189185115191共计32546244570767875068510439661221将这60户按照收入划分为10组,分析每一组的家庭消费支出。对应每周收入在80美元的5户,每周家庭消费支出在55到75美元不等。上表中,每一纵列给出的是在给定的收入水平X下的消费支出Y的分布。就是说,它给出了以X为给定值条件下的Y的条件分布。散点图根据表格的数据制成。现在,对于给定的X,例如X=80美元,有5个Y值:55、60、65、70和75美元。因此给定X=80得到这些消费支出中任何一个概率是1/5。用符号来表示:对于Y的每一条件概率分布,我们能够计算出来它的
8、均值,称为条件均值或条件期望,记做E(Y|X=Xi),并读作“在X取特定Xi值时Y的期望值”。给定X=80,Y的期望或条件均值为:51)80|55(XYp6551755170516551605155回到散点图中,我们更清楚的发现,虽然,每个家庭的消费支出都不相同,但随着收入的增加,消费水平平均地说也在增加。观测红色的粗圆点代表的Y的各个条件均值,这种察觉就更加的直观和形象。散点图表明,这些条件均值都落在一个有正斜率的直线上。这个直线叫做总体回归线。更简单地说,它是Y对X的回归。在几何意义上,总体回归线就是当解释变量取给定值时,应变量的条件均和或期望的轨迹。2.2总回归函数(PRF)从前面的讨论


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 变量 回归 分析
 优知文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
优知文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 2022自身免疫性肝炎的管理JSH临床实践指南主要内容.docx
2022自身免疫性肝炎的管理JSH临床实践指南主要内容.docx
