 专题22 锐角三角函数(讲义)(解析版).docx
专题22 锐角三角函数(讲义)(解析版).docx
《专题22 锐角三角函数(讲义)(解析版).docx》由会员分享,可在线阅读,更多相关《专题22 锐角三角函数(讲义)(解析版).docx(52页珍藏版)》请在优知文库上搜索。
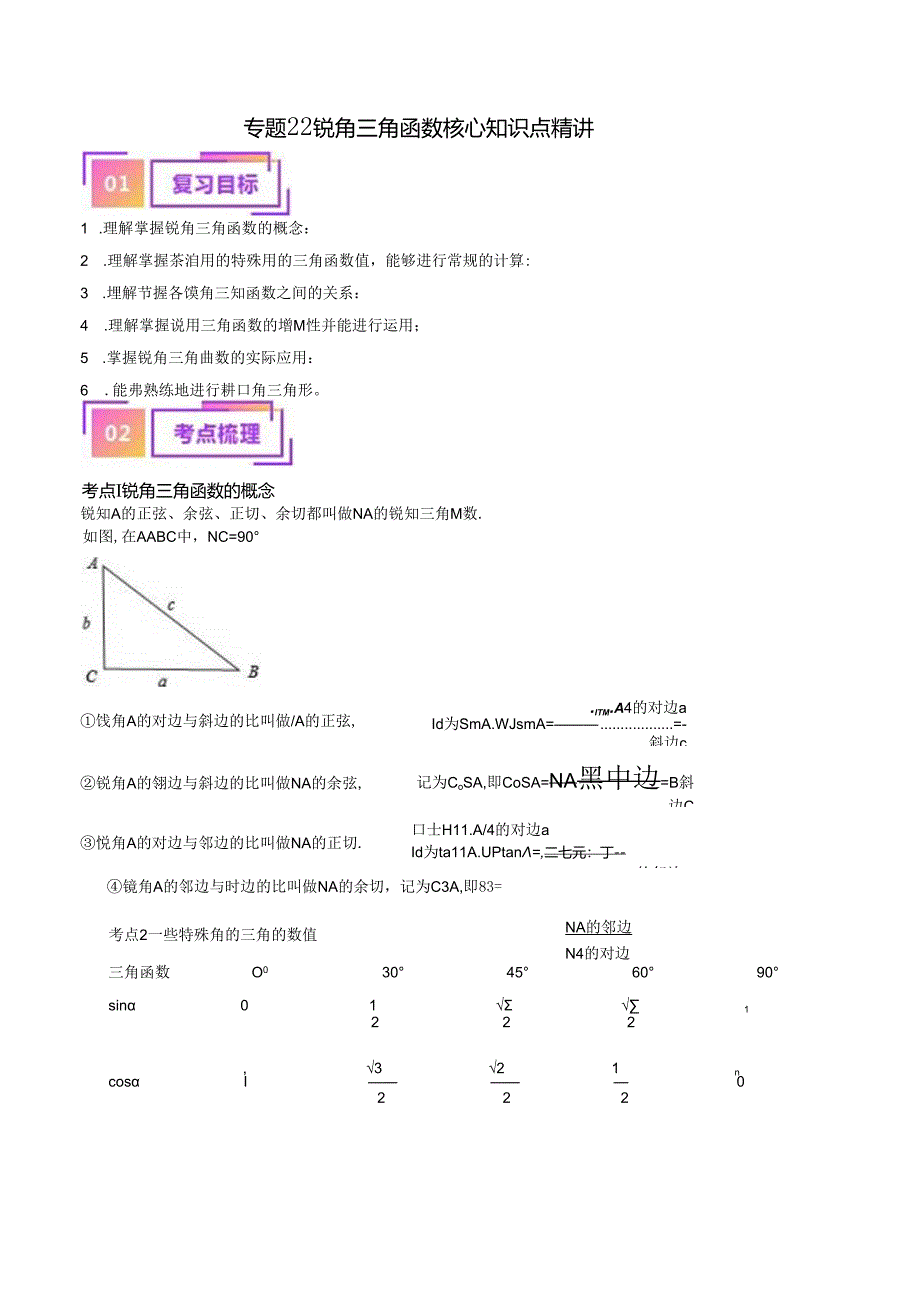
1、专题22锐角三角函数核心知识点精讲1 .理解掌握锐角三角函数的概念:2 .理解掌握茶洎用的特殊用的三角函数值,能够进行常规的计算:3 .埋解节握各馍角三知函数之间的关系:4 .理解掌握说用三角函数的增M性并能进行运用;5 .掌握锐角三角曲数的实际应用:6 .能弗熟练地进行耕口角三角形。考点I锐角三角函数的概念锐知A的正弦、余弦、正切、余切都叫做NA的锐知三角M数.如图,在AABC中,NC=90饯角A的对边与斜边的比叫做/A的正弦,.itm.a4的对边aId为SmA.WJsmA=-斜边c锐角A的翎边与斜边的比叫做NA的余弦,记为CoSA,即CoSA=NA黑中边=B斜边C悦角A的对边与邻边的比叫做
2、NA的正切.口士H11.A/4的对边aId为ta11A.UPtan=,二七元:丁-ZA的邻边b考点2一些特殊角的三角的数值三角函数O030456090sin011222,321ncosI0222镜角A的邻边与时边的比叫做NA的余切,记为C3A,即83=NA的邻边N4的对边tanaO1y3不存在3cota不存在百IO3考点3各锐角三角函数之间的关JK(1)互余关系sinA=cas(9O0A).CoSA=Sin(90A)tanA=cX(90oA).caiA=Jan90oA)(2)平方关系sin2A+cos:A=I(3)倒数关系tanAtan(900A)=1.(4)弦切关系SinAIanA=COSA
3、考点4悦角三角函数的增减性当角度在(r90。之间变化时. 1)正弦值的岩珀度的增大(或减小)而增大(或减小) 2)余花俏附着角度的增大(或减小)而减小(或增大) 3)正切值随新角度的增大(或域小)而墙大(或减小) 4)余切值随着光度的增大(或减小)而减小(或增大)考点5锐角三角函数的应用(1)仰角和倚角,在视线与水平线所成的模角中,视线在水平找上方的角叫仰角,视我在水平线卜方的角叫俯角:(2)坡度、坡角:坡度等于坡用的正切伯:(3)方向角:正北或正南方向线与目标畿所成的小于90度的角,叫做方向角.考点6解亶角三角彩1 .解宜角三角彩的桂念,在直角三角形中.除直比外.一共有五个元索,即三条边和两
4、个蜕角,山直角三角形中除直角外的已知元素求出所有未知元.我的过程叫做解直角三角形.2 .解直角三角形的理论依据;在RsABC中,ZC=90o,ZA,ZB,NC所对的边分别为a,b.C(I)三边之间的美系:a2+b2=C2(勾股定理)2)锐角之间的关系:ZA+ZB=900AB2-BC2=(2ffC)2-BC2=3fiC.AC-J1.BC3cos=Sff=1.c=T-故选:A.3.(2O23惠东县二模)已知在Rt八BC中,ZC=900.AR=5.BC=4,那么UmB的值为(4343AgB-;CgDg【答案】B【分析】根据勾股定理求出AC根楙正弦的定义计小即可.【解答】解:VZC=9(r.AB=5.
5、Bc=4.,.C=JAB2-BCi=3.an11=故选:B.3-4=C-C八K*:麓例引领rsa2特殊角的三角函数】【典例2】(2023佛山一模)在RtAA8(:中,ZC=OO0.若CoSA=今则NA的大小是(A.30【答窠】CB.450C.600D.75【分析】根据6(尸的余弦值是;解答.【解答】解:YitRsAbdWNC=90。,.,.ZA为检角,:CmA=1.A=60f故选:C.f即时检测1. (2023黄埔区校级二模)在AABC中,若ISin4-3+(日一84)2=0,则NC的度数是()A.45oB.75C.105D.120【答案】C【分析】根据非负数的件质列出关系式,根据特殊用的.用


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 专题22 锐角三角函数讲义解析版 专题 22 锐角三角 函数 讲义 解析
 优知文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
优知文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 2022自身免疫性肝炎的管理JSH临床实践指南主要内容.docx
2022自身免疫性肝炎的管理JSH临床实践指南主要内容.docx
